
Tensor Spin Observables
Since the advent of nuclear physics, all experimental results have come from only three types of measurements: decay rates, cross-sections, and spin asymmetries. Asymmetries are a ratio of cross-sections where either the beam or target (or both) have their spins aligned either with (spin-up) or against (spin-down) an external magnetic field. For example,
where σ↑(↓) are the cross-sections with spin-up (spin-down).
Tensor polarization introduces a new type measurement called a 'tensor asymmetry', described by

where σT(u) are the cross-sections with tensor polarization (T) and without polarization (unpolarized, or u).
Because of this unique measurement, we gain access to a variety of observables that are difficult or impossible to measure with any previous technique.
Currently, the Long Lab is leading two experiments to measure three of these tensor observables at Jefferson Lab: the tensor asymmetry Azz, the tensor analyzing power T20, and the tensor structure function b1.
What Is Tensor Polarization?
To talk about tensor polarization, it's helpful to first describe vector polarization, which is often just called "polarization". Due to quantum mechanics, spin-1/2 particles such as the proton have only two possible spin states called 'spin-up' and 'spin-down'. Spin-up occurs when the direction of the spin vector aligns with an external magnetic field, and spin-down occurs when the spin vector anti-aligns with the field. Vector polarization compares the number of particles in the spin-up state to the spin-down state by
Tensor polarization does not exist for spin-1/2 particles. It requires at least spin-1 systems, one of the simplest of which is a proton and neutron bound together. We call this system the 'deuteron' (deutero- for 'two' and -on for 'thing'). Again due to quantum mechanics, spin-1 particles have a spin-up and spin-down state like spin-1/2 particles, but they also have a spin-zero state. Uniquely for the deuteron, the spin-up and spin-down states (m=±1) have a different 3-dimensional structure than the spin-down (m=0) state. The animation below shows the m=±1 distribution on the left, which looks similar to a 'peanut', and the m=0 state on the right, which looks similar to a 'doughnut'.


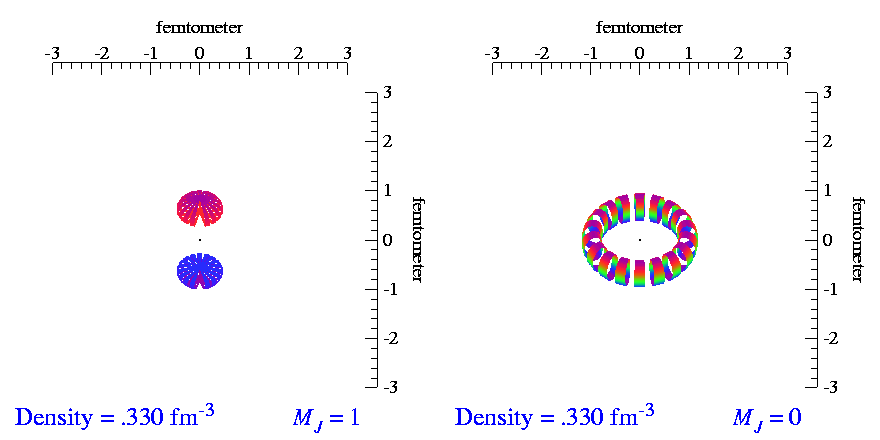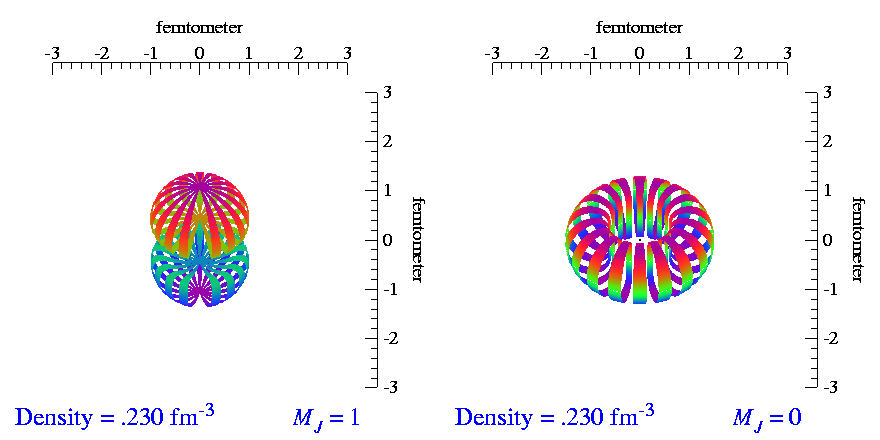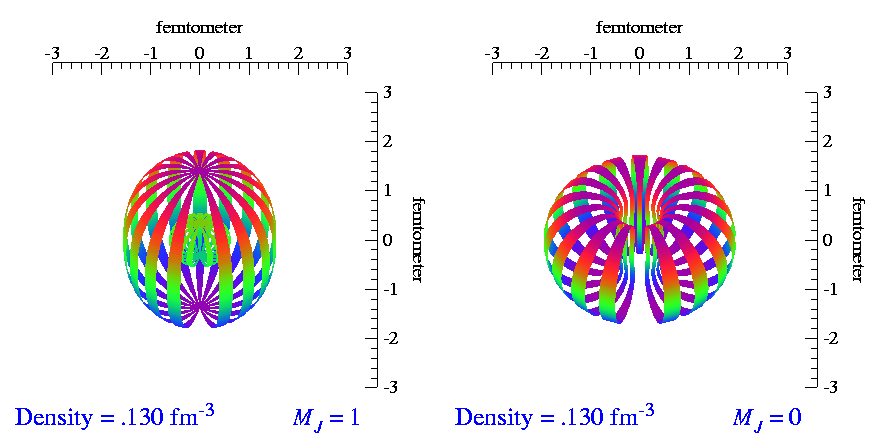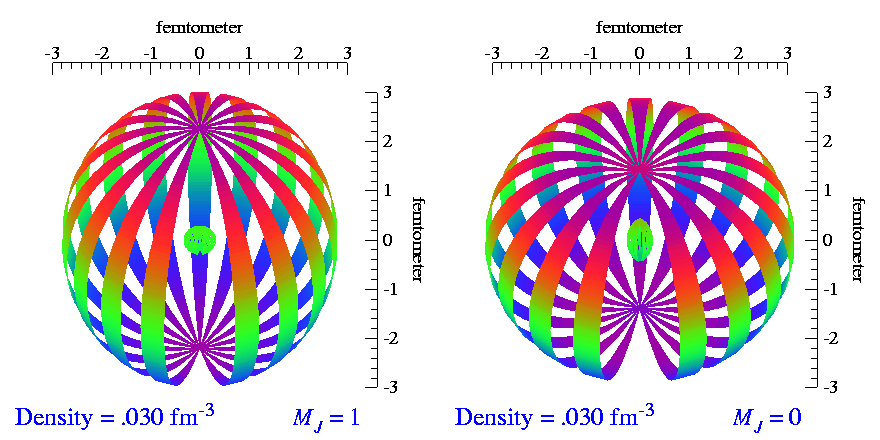
Roughly speaking, tensor polarization is a measure of whether you have more nuclei in the 'peanut' states or in the 'doughnut' state. It's given by the equation below, which is also diagrammed on the right:

The extra '2' comes from the fact that there are two types of 'peanut' states, but only one 'doughnut' state. For Pzz=0 to be unpolarized, which means there are an equal number of up, down, and zero states, the 2 is needed for normalization. If 0<Pzz≤1, there are more 'peanuts' than 'doughnuts'. If -2≤Pzz<0, there are more 'doughnuts' than 'peanuts'.



